Coaxial Cable Assembly
Microwave Test Cable
Coaxial RF Connector
Coaxial RF Adapter
Coaxial RF Termination
Coaxial RF Test Probe
Coaxial RF Attenuator
RF Switch
Coaxial RF Power Dividers
In high-frequency circuit design, calculating stripline impedance is vital for signal integrity and circuit matching. A strip line calculator impedance tool can streamline this, but understanding the process ensures better control over your designs. This article explores the problem of determining stripline impedance in ohms, analyzes the influencing factors, and provides a clear solution with a practical example, tailored for B-end users seeking reliable PCB solutions.
The Problem: Why Calculate Stripline Impedance?
Stripline impedance affects how signals travel through transmission lines in microwave circuits or PCBs. Incorrect impedance can lead to signal reflections, losses, or circuit failure. Designers need a precise method to calculate stripline Z to match components like antennas or filters. While tools like a coaxial line calculator serve coaxial cables, striplines require a distinct approach due to their planar structure. Let’s analyze the key elements involved.
Analyzing the Factors
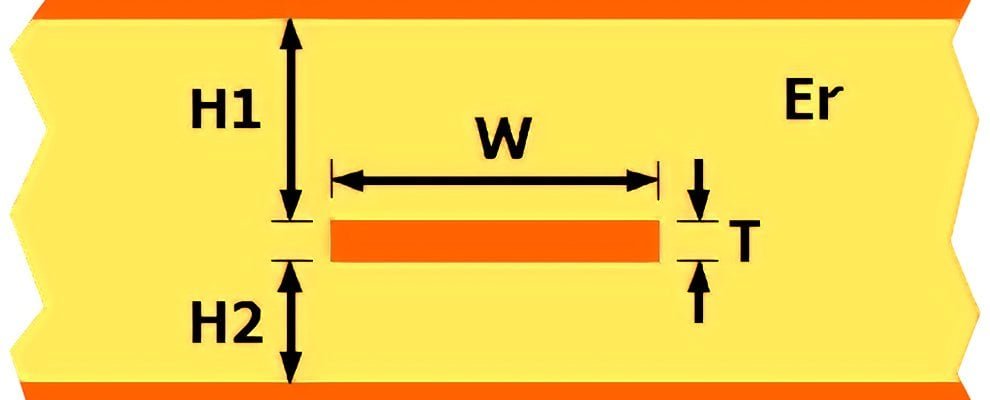
Stripline impedance depends on several parameters:
Dielectric Constant (ε_r)
The dielectric material’s relative permittivity impacts signal speed. A higher ε_r reduces impedance, common in materials like FR4 (ε_r ≈ 4.5).
Conductor Width (W)
Wider conductors lower impedance, offering more current-carrying capacity, while narrow ones increase it, suiting compact designs.
Dielectric Height (H)
The spacing between the conductor and ground planes. Greater H decreases impedance, affecting signal propagation.
Conductor Thickness (T)
Typically negligible in thin conductors, thicker ones slightly adjust impedance, critical in high-power applications.
Unlike coaxial cables—where a coaxial cable calculator uses dimensions like inner and outer diameters—striplines rely on planar geometry, making their impedance unique.
Solving the Problem: The Stripline Impedance Formula
The standard stripline impedance formula for thin conductors is:
[ Z = \frac{60}{\sqrt{\epsilon_r}} \ln\left(\frac{1.9 \times 2H}{0.8W}\right) ]
Where:
Z = Impedance in ohms
ε_r = Dielectric constant
H = Distance to each ground plane (total height/2)
W = Conductor width
This assumes T is minimal. For thicker conductors, adjust with:
[ Z = \frac{60}{\sqrt{\epsilon_r}} \ln\left(\frac{1.9 \times (2H + T)}{0.8W + T}\right) ]
The formula works when W/H > 0.35 and T/H < 0.25, common in PCB designs.
Practical Example
Consider a stripline with:
- ε_r = 4.5
- H = 0.8 mm (total height 1.6 mm)
- W = 0.3 mm
- T negligible
Steps:
- Compute ( \sqrt{4.5} \approx 2.121 )
- ( \frac{60}{2.121} \approx 28.28 )
- ( 2 \times 0.8 = 1.6 )
- ( 0.8 \times 0.3 = 0.24 )
- ( \frac{1.9 \times 1.6}{0.24} = 12.666 )
- ( \ln(12.666) \approx 2.539 )
- ( Z = 28.28 \times 2.539 \approx 71.8 , \text{ohms} )
The impedance is ~72 ohms, ideal for many RF applications.
Comparing Stripline and Coaxial Options
Unlike striplines, coaxial cables use tools like a coaxial line impedance calculator or coax impedance calculator based on coaxial cable dimensions calculator inputs (e.g., conductor diameters). Striplines excel in planar integration, while coaxial cables offer flexibility. Choose striplines for multilayer PCBs and coaxial for standalone connections.
Tips for Success
- Measure Accurately: Small errors in W or H skew results.
- Check Tolerances: PCB fabrication varies; adjust designs accordingly.
- Validate: Use simulators or a strip line calculator impedance tool to confirm manual calculations.
Avoid pitfalls like ignoring T in thick conductors or misapplying the formula outside its valid range.
Conclusion
Mastering stripline impedance calculation empowers you to design efficient, high-performance circuits. By analyzing factors and applying the formula, you achieve precise impedance control. Whether complementing a coaxial cable calculator or standalone, this knowledge drives successful PCB projects, turning inquiries into solutions.